Sobre la variación del día durante el año

Hace unos días recibí un atento comentario de un lector, que visitó mi blog, Astronomía 10° Norte, en la entrada Ecuación del tiempo y me remitió dos interesantes preguntas sobre la duración del día.
Voy a intentar una respuesta simple, pero la dividiré en dos partes.

Primero, "¿Por qué el hecho de que la tierra se desplace más rápida o más lenta en su viaje orbital influye en que el sol tarde más o menos en pasar dos veces consecutivas por el meridiano (mirando el reloj de las 24 horas)?"
En realidad considero que la pregunta es un problema de Física (Mecánica), que tiene que ver con la observación de un evento (el sol de mediodía, por ejemplo), visto desde un marco de referencia (la Tierra), que tiene un movimiento de rotación superpuesto a otro de revolución. Por eso la respuesta la doy en este blog.

Primera aproximación
Vamos a hacer la siguiente simulación, con las siguientes suposiciones:

• Usted (como si fuera la Tierra), está fijo en un cierto lugar de una explanada, desde donde puede ver las montañas del horizonte lejano (simularían las estrellas de fondo de la esfera celeste).
• A cierta distancia, quizás a 1 km, hay un objeto importante (simularía el sol).
• Usted (la Tierra), solo rota respecto a su propio eje, todo el tiempo de la misma manera, es decir con un período constante, el cual puede medir cada vez que delante de usted, en la misma dirección (digamos Sur) pasa frente a su nariz un objeto lejano (estrella) del horizonte.
• Usted comienza a medir el día (podría ser de mediodía a mediodía), cuando el objeto importante (sol), y el objeto lejano (estrella) cruzan (se alinean) su meridiano (su nariz), y termina de medir el día cuando esto ocurre la próxima vez.
  Ese sería entonces su día sideral (respecto a las estrellas), que bajo la primera aproximación también sería igual a su día solar. 
• Suponga que los midió y resultan ser 23 horas 56 minutos, 4.091 segundos.

Segunda aproximación (mejorando el modelo)

• Ahora vamos a suponer que usted (la Tierra), además de rotar, se va a mover unos cuantos pasos en el mismo sentido de la rotación, simulando que realiza una revolución, respecto al objeto importante (el sol). Esto es, simule que da una vuelta alrededor del Sol, pero en una órbita circular, a una distancia constante del Sol, que tendrá que recorrer manteniendo una rapidez constante, debido a que la fuerza de atracción entre usted y el objeto (fuerza de gravitación) es constante. Si realmente usted fuera la Tierra, daría una vuelta (una revolución) en 365.256363004 días.
• Trate de hacerlo de la siguiente manera: inicie cuando el sol y la estrella de referencia realizan un tránsito, ambos alineados justamente frente a su nariz (como en la primera aproximación). Luego, mientras usted considera que transcurre un día, aléjese unos 30 pasos hacia la derecha, para encontrar el siguiente tránsito de la estrella y del Sol, que le definirán el tamaño de un día.
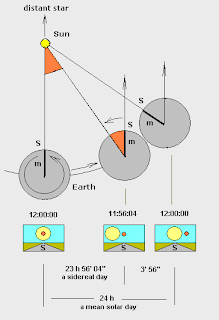
• Encontrará que primero transita la estrella frente a su nariz (exactamente al Sur como al principio) y su cronómetro leerá: 23 horas, 56 minutos, 4.091 segundos.
• Pero debido a que ha rotado un cierto ángulo (360°/365,25 días), aún no transita el objeto importante (sol). Notará que tiene que rotar un poquito más.
  El Sol transitará, definiendo esa particular duración del día hasta que el cronómetro marque 24 horas.
• Eso sucederá cada día de los 365.25 días de la revolución de la Tierra alrededor del Sol, puesto que el inicio y final de cada día son equivalentes, siempre que la órbita sea circular y se recorra con rapidez constante. 
• Observe que, por su definición, este día solar es entonces unos cuatro minutos mayor que el día sideral, pero todos serían iguales durante el año.

Tercera aproximación (más cerca de la realidad)

• Ahora vamos considerar que la órbita de la Tierra es una elípse, cuya consecuencia más importante en este caso es que usted (la Tierra), realizará la revolución con rapidez variable.
  Cerca del perihelio (como el 4 de enero) su rapidez (30 300 m/s) es mayor que la rapidez promedio (29 780 m/s) y cerca del afelio (como el 4 de julio), su rapidez (29 300 m/s) es menor. 
• Si lo simula, lo cual debe hacer con cierto cuidado, tendrá que a veces  dar unos, digamos 50 pasos (perihelio) y a veces unos 10 pasos.
  
  Pero estoy seguro que su razonamiento de la situación le hace concluir que el día solar a lo largo del año tiene diferente duración.
  
• Bueno, precisamente el promedio de estas variaciones es lo que llamamos el día solar medio, unas 24 horas, o 86 400 segundos. Promedio, porque cada día tiene ligeramente diferente duración.

La cuarta aproximación a la realidad (la Tierra rota con un eje inclinado respecto al plano de la órbita), la dejaremos para una nueva entrada. 

Por ahora me gustaría recibir comentarios, otras explicaciones, etc.
Gracias
Jav