La fuerza de rozamiento 🎵 "Papel de lija" (póngale volumen)
Si usted ha lijado alguna vez una superficie, posiblemente ha encontrado alguno de los siguientes resultados:
 |
- Entre la superficie que está lijando y el papel de lija, resulta una fuerza ¡paralela a ambas superficies!
- Esta fuerza siempre tiene dirección opuesta al movimiento relativo de las dos superficies.
- Si usted lija hacia la izquierda la citada fuerza (sobre el papel de lija) es hacia la derecha y viceversa.
- Depende
de la rugosidad de la pareja de superficies
en contacto, mientras más rugosas mayor es la fuerza, por eso, según el
resultado que queramos, usamos lija ordinaria, mediana, o fina.
- Depende de la fuerza con que se comprimen las dos superficies.
- A mayor fuerza de compresión mayor fuerza de rozamiento.
Los físicos e ingenieros llamamos a esta fuerza, la fuerza de rozamiento por deslizamiento.
La
fuerza de rozamiento puede ser molesta, por ejemplo, cuando empujamos una
pesada caja sobre el piso. Pero, aunque usted no lo crea, sin ella no podríamos
caminar, y las llantas de los autos y la carretera no podrían desarrollar
suficiente tracción para que esta los impulse hacia adelante.
Podemos disminuir el rozamiento hasta un cierto punto, puliendo las superficies
y colocando lubricante entre ellas, o por medio de rodines, pero no se puede
eliminar completamente.
Cuando usted estaciona un vehículo en una pendiente, el mérito no es únicamente del freno de mano, que solamente evita que las ruedas giren. (lo más aconsejable es colocar una cuña como calza).
La fuerza de rozamiento que ejerce la carretera hacia arriba de la pendiente es la que contrarresta exactamente (¡ni más ni menos!) el efecto del peso del vehículo, que de otra manera se deslizaría hacia abajo.
Si
el peso del vehículo aumenta, o el ángulo de la pendiente crece, la fuerza de
rozamiento que se requiere, no es suficiente, -pues tiene un valor máximo-.
Entonces el vehículo no logrará mantenerse en reposo y se deslizará
inevitablemente hacia abajo. Esto les ha sucedido a camiones muy cargados
mientras suben una pendiente y por algún motivo se les ha apagado el motor. No
ha habido freno de pedal ni freno de mano que los sostenga. Tenga cuidado,
porque conducir correctamente hacia atrás un carro que se resbala por una
pendiente, no es nada fácil.
Bueno,
simplemente restablecer la fuerza de rozamiento a valores aceptables. El
problema no es la fuerza que comprime las llantas y el lodo. El problema es la
poca rugosidad entre éstas. Lo que hay que hacer es colocar alguna superficie
rugosa entre las llantas y el lodo (cadenas a las llantas, una capa de piedras,
o piezas de madera, que permitan un mayor rozamiento entre las superficies.).
¡Debe conducir lentamente en la marcha más baja!
Finalmente, una pregunta para que la analice aquí, y la ponga en práctica más adelante.
En
uno de esos juegos de tirar de la cuerda entre dos personas (o dos grupos),
suponga que compiten un atleta musculoso de 90 kg y un gordito no muy fuerte de
150 kg. Si ambos usan zapatos con suelas idénticas y el piso es homogéneo,
¿quién tiene mayor probabilidad de ganar?
Equilibrio estático
Todo
objeto que se fabrique o construya; desde un banco para sentarse, hasta una
casa, un edificio o un puente, debe estar en equilibrio estático y dinámico,
para que la estructura no colapse y se pueda usar con confianza por muchos
años.
Cuando
usted ordena los planos de su casa, el arquitecto y el ingeniero deben revisar
eso muy bien, además de cosas como la resistencia de materiales, análisis de
suelos, etc.
¡Va incluido en lo que usted paga!
En el caso de estructuras fijas, (que deben estar en reposo):
El
equilibrio estático requiere que todas las fuerzas externas a la estructura
se cancelen entre sí, esto es que sumen cero.
Además,
se requiere que la suma de esas fuerzas no presente una tendencia
desbalanceada a hacer girar la estructura, lo cual requiere una condición
adicional más compleja, la de equilibrio rotacional, que de momento no
trataremos aquí.
En una situación unidimensional, por ejemplo, si usted está colgando verticalmente de una barra de ejercicios que a su vez cuelga del techo de su casa, podemos ponerle atención a usted, como el cuerpo de interés, o a las dos cuerdas, e inclusive a los soportes del techo,.
Si usted está colgado en reposo (en equilibrio estático), la fuerza de su peso (masa en kg × 9,8 N/kg) debe ser equilibrada por las dos fuerzas que la barra ejerce hacia arriba sobre sus dos manos. La suma de estas fuerzas verticales debe ser igual a cero.
Si
analizamos la barra; las dos fuerzas hacia arriba que ejercen las cuerdas deben
ser equilibradas por la fuerza del peso de la barra y la que ejercen sus dos
manos (esencialmente su peso), hacia abajo. La suma de fuerzas verticales
debe ser igual a cero.
Si analizamos la cuerda que está en el extremo izquierdo de la barra; la fuerza hacia arriba que hace el soporte en el techo debe ser igual a la fuerza que el extremo izquierdo de la barra ejerce hacia abajo, que debe tomar en cuenta de alguna manera su peso y el peso de la barra. La suma de fuerzas verticales debe ser igual acero.
Si
analizamos los músculos y articulaciones de sus dos hombros; la fuerza que
ejerce cada brazo hacia arriba debe ser igual a la mitad de su peso (si hay
simetría en la posición). La suma de fuerzas verticales es igual a cero.
Ahora veamos un caso bidimensional. Suponga que tiene colgada una maceta de 10 kg por medio de las tres cuerdas de peso despreciable A, B, C, como se muestra en la figura y queremos saber cuánto es la fuerza de tensión que está soportando cada cuerda.
Tomemos
como objeto en equilibrio estático -al
nudo- donde se juntas las tres cuerdas-.
Con
solo mirar, concluimos que la tensión de la cuerda C es igual al peso de la
maceta (98 N), que tira de ella hacia abajo desde su extremo inferior y es
halada hacia arriba por el nudo.
La
cuerda B, supuestamente horizontal ejerce una fuerza hacia la izquierda sobre
el nudo, igual a la fuerza de tensión a la hace la pared (si la masa de la
cuerda es despreciable).
La
cuerda A, ejerce una fuerza sobre el nudo, a lo largo de ella; cierta magnitud
hacia arriba y cierta magnitud hacia la izquierda. Para que el nudo esté en
equilibrio debe cumplirse que:
La
suma de fuerzas horizontales debe ser igual a cero:
fuerza B + componente horizontal de fuerza A = 0.
La
suma de fuerzas verticales debe ser igual a cero:
Fuerza C + componente vertical de fuerza A = 0.
Estas
dos ecuaciones con dos incógnitas permiten mediante una manipulación matemática
simple, encontrar la tensión de las cuerdas B y A.
En un caso tridimensional, si queremos equilibrio estático, simplemente debemos comprobar por ejemplo que:
Suma
de fuerzas Norte-Sur = 0
Suma
de fuerzas Este- Oeste = 0
Suma
de fuerzas arriba-abajo = 0
Centro de masa
El
concepto de centro de masa tiene sentido, solo en el caso de un cuerpo formado
por dos o más partículas, pues si solo fuera una, ella misma es (o está) en su
centro de masa.
El centro de masa de un sistema discreto (partículas separadas) o continuo (de densidad uniforme) es el punto geométrico que dinámicamente se comporta como si en él estuviera aplicada la resultante de las fuerzas externas al sistema.
Esto
permite aplicarle a dicho cuerpo, para su análisis dinámico, las leyes de la
física, de una manera más simple.
En
el caso de dos partículas idénticas (en masa), su centro de masa está en el
punto medio entre ellas.
Pero
si las partículas tienen masa diferente, evidentemente el
centro de masa estará más cercano a la partícula de mayor masa.
Tal es el caso del centro de masa del sistema Tierra-Luna, en que el centro de masa está a 4671 km del centro de la Tierra, ¡dentro de la Tierra misma!, ya que su radio es 6378 km, su masa es 81 veces la masa de la Luna, y la distancia promedio entre los centros de los dos cuerpos es 384 402 km.
Determinar
el centro de masa de un conjunto de cuerpos requiere un cálculo matemático
semejante al de obtener un promedio de calificaciones, pero en la que cada una
de ellas tiene un valor porcentual diferente que debe tomarse en cuenta. Evidentemente
los cuerpos con mayor masa aportarán más que los de menor masa. Algo así como
el resultado de sumar (m1)(d1) + (m2)(d2) + … todo dividido por la masa total.
Escogiendo
un marco de referencia apropiado y haciendo el cálculo para cada uno de los tres
ejes, en el caso de un cuerpo tridimensional.
(https://fisica1011tutor.blogspot.com/2011/02/centro-de-masa-del-sistema-solar.html)
Para
una distribución de masa compleja y dinámica como el Sistema Solar, la
determinación del centro de masa puede realizarse aplicando la matemática
apropiada. Encontrará, sin embargo, que no dista mucho del centro del Sol, como
podría esperarse, debido a que la estrella aporta la mayor cantidad de
masa.
Centro
de gravedad
Para propósitos simples de física e ingeniería, en el centro de gravedad se considera que actúa el peso total del cuerpo.
El centro de gravedad no necesariamente es un punto real del cuerpo, puede estar fuera de él, como en el caso de algunas figuras planas simples; un transportador, una letra L, un anillo, un cascarón esférico, una persona que se inclina hacia un lado, etc.
Si
el cuerpo en estudio está en un campo gravitatorio constante, como el que
experimentamos en una región particular de la Tierra, el centro de gravedad y
el centro de masa coinciden.
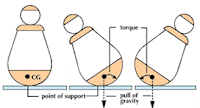
Para el equilibrio de un cuerpo, mientras más bajo esté el centro de gravedad, respecto a la superficie horizontal que lo soporta, mayor será su estabilidad.
Para
un cuerpo que descansa en soportes, como un carro, una escalera, y aún una
persona, la vertical del centro de gravedad hacia abajo, debe caer dentro de la
superficie de soporte del cuerpo. Si cae fuera de ella, el torque (vea sección
14 del peso podrá volcar al cuerpo.
https://www.youtube.com/watch?v=R8wKV0UQtlo14.
No hay comentarios.:
Publicar un comentario