La interpretación del comportamiento de la luz como una partícula (fotón) o como una onda es bastante antigua y en algunos momentos ha prevalecido entre los físicos uno u otro criterio. Diversos científicos han aportado sus opiniones y experimentos para probar el comportamiento corpuscular o el ondulatorio, aunque parece que no ambos simultáneamente.
¿A usted que le parece, se comporta la luz como una onda o como una partícula?
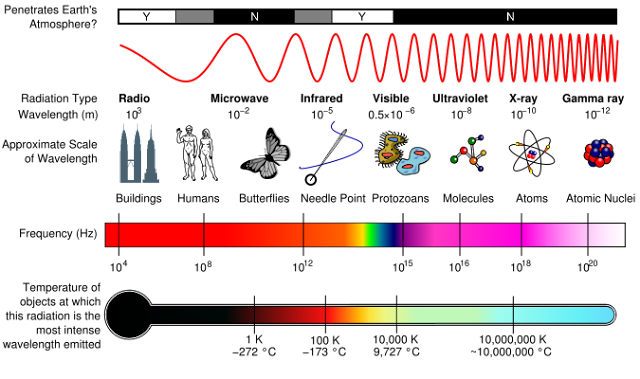
(http://www.williams.edu/astronomy/Course-Pages/111/Images/ems.jpg)
Primero aclaremos que para la ciencia en general y para la física en particular, cuando se habla de luz normalmente se hace referencia a todo el espectro electromagnético.
Cuando de manera específica se trata de la región de dicho espectro capaz de estimular el sentido de la vista, entonces decimos luz visible o espectro visible. Por tal motivo, algunas características y propiedades que citaremos aquí, son comunes a los rayos gamma, los rayos x, los rayos ultravioleta, la luz visible, los rayos infrarrojos, las micro ondas y las ondas de radio.
ondas y las ondas de radio.
Primero aclaremos que para la ciencia en general y para la física en particular, cuando se habla de luz normalmente se hace referencia a todo el espectro electromagnético.
Cuando de manera específica se trata de la región de dicho espectro capaz de estimular el sentido de la vista, entonces decimos luz visible o espectro visible. Por tal motivo, algunas características y propiedades que citaremos aquí, son comunes a los rayos gamma, los rayos x, los rayos ultravioleta, la luz visible, los rayos infrarrojos, las micro
 ondas y las ondas de radio.
ondas y las ondas de radio.
Posiblemente comenzamos intuitivamente aceptando el modelo corpuscular de la luz, ya que la formación de sombras y la reflexión, pareciera que se pueden explicar fácilmente como si de la fuente luminosa salieran microscópicos corpúsculos, viajando en línea recta.
La reflexión especular de la luz, uno de los fenómenos más cotidianos, parece responder a un comportamiento semejante a las colisiones elásticas de bolas de billar contra la banda de la mesa. Lo único que nos falta para ser fieles creyentes del modelo corpuscular sería tener la capacidad de percibir los invisibles fotones, saliendo disparados de la fuente como si fuera una microscópica ametralladora y verlos rebotar en un espejo, con el mismo ángulo que llegan y en el mismo plano, lo cual puede usted simular fácilmente con un puntero láser.
La reflexión especular de la luz, uno de los fenómenos más cotidianos, parece responder a un comportamiento semejante a las colisiones elásticas de bolas de billar contra la banda de la mesa. Lo único que nos falta para ser fieles creyentes del modelo corpuscular sería tener la capacidad de percibir los invisibles fotones, saliendo disparados de la fuente como si fuera una microscópica ametralladora y verlos rebotar en un espejo, con el mismo ángulo que llegan y en el mismo plano, lo cual puede usted simular fácilmente con un puntero láser.
Reflexión xxxxxxxxxxxxxxxxxxxxxxRefracción
Entre los proponentes famosos de la teoría corpuscular debemos citar a Isaac Newton, quien publicó en 1704 el libro Optiks, donde presenta diversos resultados de sus investigaciones sobre la luz.
Es importante anotar aquí que en 1676 Ole Rømer realizó una medición de la velocidad de la luz, basada en el cambio del periodo de los eclipses del satélite Io de Júpiter, obteniendo el valor de 214 000 km/s.
También hay varias mediciones de Albert Michelson (299 796 ± 0,4 km/s, en 1926) y de otros investigadores. El valor aceptado actualmente es 299 792, 458 km/s, basado en una medición con láser de 1973.
También hay varias mediciones de Albert Michelson (299 796 ± 0,4 km/s, en 1926) y de otros investigadores. El valor aceptado actualmente es 299 792, 458 km/s, basado en una medición con láser de 1973.
Sin embargo, ya en 1690 Christian Huygens proponía la naturaleza ondulatoria de la luz en su libro Traité de la lumière , en el cual explica la propagación rectilínea, la reflexión y la refracción de la luz, basando su discusión en que la luz es una perturbación que viaja de la fuente al detector, que transmite energía sin que haya transporte de materia, en cierta manera similar a la propagación de las ondas sonoras.
Luego en 1817 Thomas Young y en 1820 Augustine Fresnel realizaron experimentos sobre difracción, interferencia y polarización de la luz, que dieron el reconocimiento necesario para aceptar definitivamente su comportamiento ondulatorio.
 Interferencia: (http://commons.wikimedia.org/wiki/File:Two_sources_interference.gif)
Interferencia: (http://commons.wikimedia.org/wiki/File:Two_sources_interference.gif)
En 1861 James C. Maxwell da a conocer un conjunto de cuatro ecuaciones, conocidas hoy como ecuaciones de Maxwell en las que además relaciona la velocidad de la luz en el vacío con propiedades del campo magnético y del campo eléctrico, por lo que la luz pasa a ser una onda electromagnética.
Y en 1887 Heinrich Hertz demostró que las ondas de radio son ondas electromagnéticas.
Y en 1887 Heinrich Hertz demostró que las ondas de radio son ondas electromagnéticas.
Creo que a partir de ahí la naturaleza ondulatoria de la luz quedó plenamente establecida y confirmada.
¿Pero que es una onda electromagnética, que es lo que vibra u oscila en un rayo luminoso?
Primero una revisión rápida sobre ondas mecánicas.
Son las que necesitan un medio para propagarse y es este medio el que vibra cuando la onda lo atraviesa.
Un ejemplo son las ondas sonoras, que son ondas mecánicas longitudinales, en las que el medio (digamos el aire entre la boquilla de una flauta y nuestros tímpanos) experimenta compresiones y rarefacciones en la misma dirección en que viaja la onda.
Un ejemplo son las ondas sonoras, que son ondas mecánicas longitudinales, en las que el medio (digamos el aire entre la boquilla de una flauta y nuestros tímpanos) experimenta compresiones y rarefacciones en la misma dirección en que viaja la onda.
Usted puede producir fácilmente ondas longitudinales en un resorte tenso, recogiendo unas cuantas vueltas y luego soltándolas.
También hay ondas mecánicas transversales, como las que ocurren en una cuerda de guitarra, o las que usted puede generar fácilmente azotando un mecate arriba-abajo, o izquierda derecha.
Las ondas sísmicas, pueden ser longitudinales (P) o transversales (S).
Las ondas sísmicas, pueden ser longitudinales (P) o transversales (S).
Las ondas electromagnéticas no son ondas mecánicas, no necesitan ningún medio para propagarse, aunque pueden hacerlo a través de algunos.
La luz y todas las ondas del espectro electromagnético se propagan en el vacío y además son ondas transversales.
Si recuerda su experiencia con las ondas transversales con un mecate, quizás se dio cuenta que las puede polarizar, es decir que la vibración perpendicular a la dirección de propagación la puede mantener en el plano vertical o en el horizontal (polarizarla), una característica exclusiva de las ondas transversales.
Las ondas electromagnéticas son ondas transversales y lo que oscila, vibra u ondula es el campo eléctrico y el campo magnético asociado al tipo particular de onda.
Además, las ondas electromagnéticas pueden polarizarse.
Además, las ondas electromagnéticas pueden polarizarse.
Si usted se imagina que un rayo luminoso avanza en la dirección del pulgar extendido de su mano derecha (figura), entonces el campo eléctrico de la onda vibra en la dirección de su dedo central y el campo magnético en la dirección de su dedo índice, todos a 90° entre sí (regla de la mano derecha).
¿Listo entonces para aceptar que la luz visible y el resto de sus amigas son ondas y no partículas? Bueno no tan rápido, veamos otros experimentos.
En 1887 Heinrich Hertz observa y describe lo que llamamos ahora efecto fotoeléctrico, esto es la emisión de electrones por un material cuando se le ilumina con radiación electromagnética de longitud de onda corta como visible o ultravioleta. En 1901 Nikola Tesla lo redescubre y es el primer científico que lo describe en términos de partículas.
En 1905 Albert Einstein provee una explicación del efecto fotoeléctrico en términos de cuantos de energía luminosa (fotones) con propiedades de partículas. No tienen masa (masa en reposo), pero poseen cantidad de movimiento (p = h f/c = h/λ) y una cantidad discreta de energía relacionada con su frecuencia (E= h f = h c/λ), donde h = 6,626 x 10-34 joule segundo es la llamada constante de Planck.
Finalmente citaré que en 1923 Arthur Holly Compton observó un proceso de interacción entre electrones y rayos gamma, el cual solo se puede explicar satisfactoriamente en términos de la conservación de la energía y de la cantidad de movimiento de fotones y electrones, usando las expresiones relativistas (http://fisica1011tutor.blogspot.com/2009/10/relatividad-especial-iv-energia.html).
(http://fisica1011tutor.blogspot.com/2009/09/cantidad-de-movimiento).
(http://fisica1011tutor.blogspot.com/2009/09/cantidad-de-movimiento).
Los fotones también son apropiados para describir el fenómeno de aniquilación partícula-antipartícula, y en la creación de pares.
¿Qué piensa usted ahora de la luz?
Bueno, al final seguro a la luz no le importa, siempre hará su trabajo, para que podamos percibir la natualeza que compartimos; lo hermoso de lo feo y lo sublime de lo bello.
Espero no haberla(lo) confundido mucho.
La citas del texto y las referencias adicionales puede serle de mucha ayuda para aclarar sus dudas.
Referencias adicionales:
http://es.wikipedia.org/wiki/Historia_de_la_electricidad